Simulation of genetic values based on a compound symmetry model for genotype-by-environment (GxE) interaction

Background

This document demonstrates how to simulate genetic values for multiple traits in multiple environments based on a compound symmetry model for genotype-by-environment (GxE) interaction, assuming a separable structure between traits and environments. While the simulation of genetic values is not directly implemented in ‘FieldSimR’, the package provides wrapper functions to facilitate the simulation of genetic values for multi-environment field trial settings employing the R package ‘AlphaSimR’. The two wrapper functions to simulate genetic values based on a compound symmetry GxE interaction model are:

• compsym_asr_input()
• compsym_asr_output()

Note: ‘FieldSimR’ also provides wrapper functions to enable simulation of genetic values based on an unstructured model for genotype-by-environment (GxE) interaction. This is demonstrated in the vignette on the Simulation of genetic values based on an unstructured model for genotype-by-environment (GxE) interaction.

The core function of ‘FieldSimR’ generates plot errors comprising 1) a spatially correlated error term, 2) a random error term, and 3) an extraneous error term. Spatially correlated errors are simulated using either bivariate interpolation, or a two-dimensional autoregressive process of order one (AR1:AR1). Through the combination of the plot errors with (simulated) genetic values, ‘FieldSimR’ enables simulation of multi-environment plant breeding trials at the plot. This is demonstrated in the vignette on the Simulation of plot errors and phenotypes in a plant breeding field trial.

Simulation of genetic values

We conceive a scenario in which 100 maize hybrids are measured for grain yield (t/ha) and plant height (cm) in three environments. The first and the third environment include two replicated, and the second environment includes three replicates

The simulation process comprises three steps:

1. Definition of the genetic architecture and the simulation parameters for the two traits.
2. Simulation of a population of 100 hybrid genotypes.
3. Generation of a data frame containing the simulated genetic values for grain yield and plant height in the three environments..

To provide a comprehensive overview of the compound symmetry modelling approach for GxE interaction, we assume additive and dominance gene action for both grain yield and plant height. Details on how ‘AlphaSimR’ simulates additive and non-additive biological effects can be found in the “Traits in AlphaSimR” vignette.

It should be noted, however, that a simple additive genetic model will be sufficient to answer most experimental questions and may be preferred to more complex models, especially if data to tune the simulation model is not available and the parameters are unknown.

1. Genetic architecture and simulation parameters of the two traits

First, we set the number of traits, the number of environments (e.g., locations), and the number of replicates tested within environments. We also define the number of genotypes in our founder population to be simulated, the number of chromosomes, and the number of segregating sites (biallelic QTN) per chromosome. Then, we set the additive genetic parameters, the dominance parameters, and the genetic correlation structures required to simulate the two traits in three environments based on a compound symmetry model for GxE interaction.

We create a founder population of 20 heterozygous genotypes. These founder genotypes will then be split into two heterotic pools, and one doubled haploid (DH) line will be produced from each founder. To generate hybrids, the two pools will be crossed using a factorial design.

ntraits <- 2 # Number of traits.
nenvs <- 3 # Number of environments.
nreps <- c(2, 2, 3) # Number of replicates of each genotype in environments 1, 2, and 3.


nind <- 20 # Number of founder genotypes in the population.
nchr <- 10 # Number of chromosomes.
nseg_sites <- 200 # Number of QTN per chromosome.

Additive genetic parameters

We define mean additive genetic values for all trait x environment combinations. The additive mean values are provided in a single vector with environments nested within traits. Grain yield is measured in tons per hectare (t/ha) and plant height is measured in centimetres (cm).

mean <- c(4.9, 5.4, 5.1, 235.2, 228.5, 239.1) # c(Yld:E1, Yld:E2, Yld:E3, Pht:E1, Pht:E2, Pht:E3)

Simulated traits are restricted by the compound symmetry model to having the same genetic variance for each environment (genotype main effect variance + GxE interaction variance) and the same genetic covariance between each pair of environments (genotype main effect variance).

var <- c(0.08, 13) # c(grain yield, plant height)

The proportion of main effect variance for each trait also defines the total genetic correlation between the environments in the compound symmetry model.

prop_main <- c(0.4, 0.6) # c(grain yield, plant height)

Additive genetic correlations between the two traits are set in a 2x2 correlation matrix.

corA <- matrix( # Matrix of additive genetic correlations grain yield and plant height.
  c(
    1.0, 0.5,
    0.5, 1.0
  ),
  ncol = 2
)

#>      [,1] [,2]
#> [1,]  1.0  0.5
#> [2,]  0.5  1.0

Dominance genetic parameters

Dominance degrees and dominance degree variances for the two traits are defined in the same way. We assume independence between the dominance degrees of grain yield and plant height. Therefore, we generate a 2x2 diagonal matrix (although this is not strictly necessary. A diagonal matrix is constructed by default if no correlation matrix is provided).

meanDD <- c(0.4, 0.4, 0.4, 0.1, 0.1, 0.1) # c(Yld:E1, Yld:E2, Yld:E3, Pht:E1, Pht:E2, Pht:E3)

varDD <- c(0.2, 0.2) # c(grain yield, plant height)

prop_mainDD <- 0.4 # Same value set for traits 1 and 2.

corDD <- diag(2)

#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1

Input parameter list

Once we have defined all simulation parameters, we use the function compsym_asr_input() to prepare them into a list that is used with ‘AlphaSimR’ to simulate correlated genetic values based on a compound symmetry model for GxE interaction.

input_asr <- compsym_asr_input(
  ntraits = ntraits,
  nenvs = nenvs,
  mean = mean,
  var = var,
  prop.main = prop_main,
  corA = corA,
  meanDD = meanDD,
  varDD = varDD,
  prop.mainDD = prop_mainDD,
  corDD = corDD
)

Note: The object input_asr should not be modified and must be used directly with ‘AlphaSimR’ as demonstrated below.

2. Simulation of a population of genotypes

Our list of simulation parameters input_asr is now used with ‘AlphaSimR’ to simulate correlated genetic values for 100 maize hybrid genotypes tested for two traits in three environments based on a compound symmetry model for GxE interaction.

First, we simulate a population of 20 heterozygous maize founder genotypes using the function runMacs in ‘AlphaSimR’.

founders <- runMacs( # Simulation of founder genotypes using AlphaSimR's "MAIZE" presets
  nInd = nind, # to mimic the species' evolutionary history.
  nChr = nchr,
  segSites = nseg_sites,
  species = "MAIZE",
  nThreads = 2
)

SP <- SimParam$new(founders)

Then, we use the simulation parameters stored in input_asr to simulate correlated genetic values for grain yield and plant height in three testing environments.

SP$addTraitAD( # Additive + dominance trait simulation.
  nQtlPerChr = nseg_sites,
  mean = input_asr$mean,
  var = input_asr$var,
  corA = input_asr$corA,
  meanDD = input_asr$meanDD,
  varDD = input_asr$varDD,
  corDD = input_asr$corDD,
  useVarA = FALSE
)

founders <- newPop(founders)

We now split the simulated founders into two heterotic pools A and B. We create one DH line per founder, which gives us 10 DH lines per heterotic pool. Hybrids are then generated by crossing pool A and pool B in a factorial manner (all pairwise combinations), resulting in 100 hybrid genotypes

pool_A <- makeDH(founders[1:10], nDH = 1) # Pool A: 1 DH line from founders 1 to 10, respectively.
pool_B <- makeDH(founders[11:20], nDH = 1) # Pool B: 1 DH line from founders 11 to 20, respectively.

dh_lines <- mergePops(list(pool_A, pool_B))

factorial_plan <- as.matrix(expand.grid(A = pool_A@id, B = pool_B@id)) # Factorial crossing plan.

hybrid_pop <- makeCross(pop = dh_lines, crossPlan = factorial_plan, nProgeny = 1) # Hybrid genotypes.

3. Generation of a data frame with simulated genetic values

In the last step, we use the function compsym_asr_output() to extract the simulated genetic values from the ‘AlphaSimR’ population object hybrid_pop and store them in a data frame.

gv_df <- compsym_asr_output(
  pop = hybrid_pop,
  ntraits = ntraits,
  nenvs = nenvs,
  nreps = nreps
)

#>   env id rep gv.Trait1 gv.Trait2
#> 1   1 41   1  4.964078  240.7900
#> 2   1 42   1  4.597894  237.0043
#> 3   1 43   1  5.090570  237.3167
#> 4   1 44   1  4.816378  236.7378
#> 5   1 45   1  4.212023  230.0102
#> 6   1 46   1  4.773841  236.1104

Histogram showing the genetic values of the 100 maize hybrids for grain yield in the three environments

ggplot(gv_df, aes(x = gv.Trait1, fill = factor(env))) +
  geom_histogram(color = "#e9ecef", alpha = 0.8, position = "identity", bins = 50) +
  scale_fill_manual(values = c("violetred3", "goldenrod3", "skyblue2")) +
  labs(x = "Genetic values for grain yield (t/ha)", y = "Count", fill = "Environment")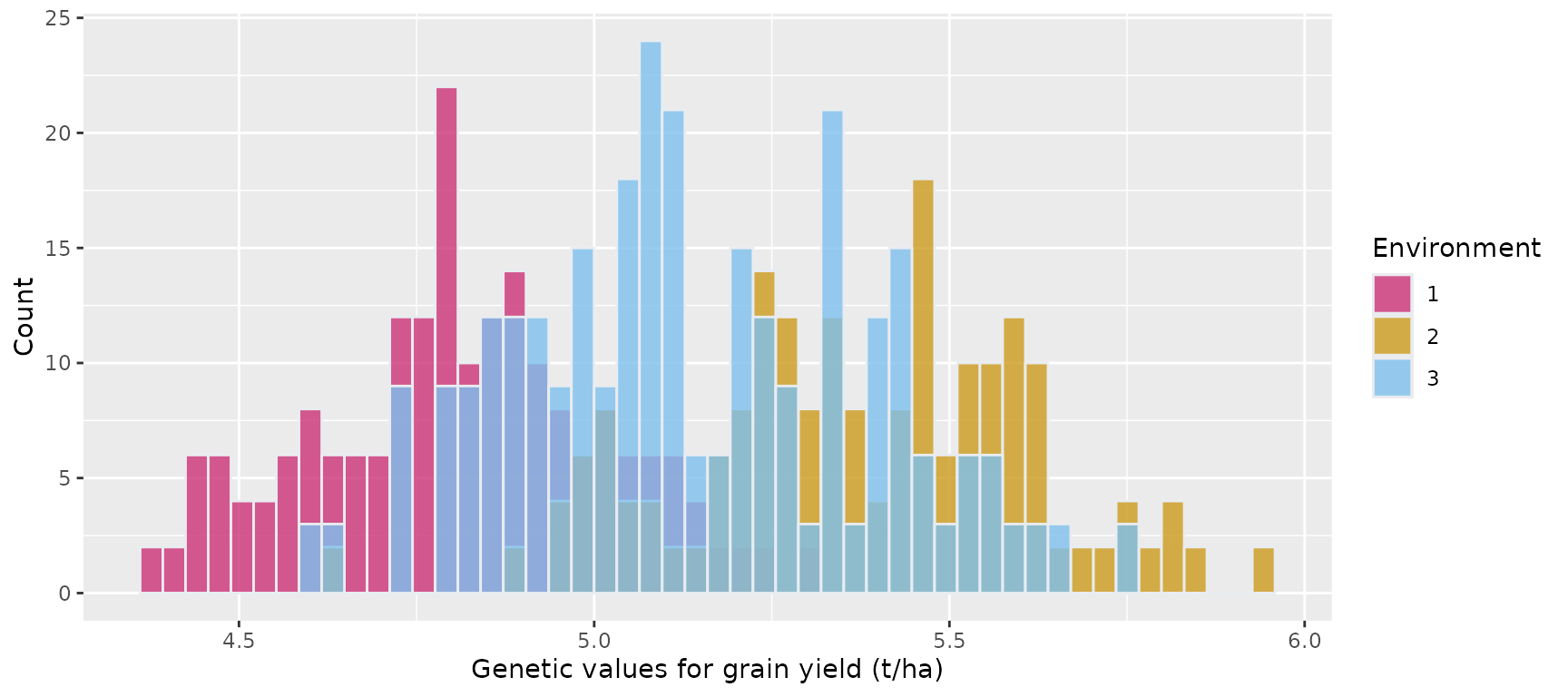

The simulated genetic values for grain yield and protein content measured at three environments can now be combined with plot errors to generate plant breeding trial phenotype data at the plot. We provide an example on how to do that in the vignette Simulation of plot errors and phenotypes in a plant breeding field trial.